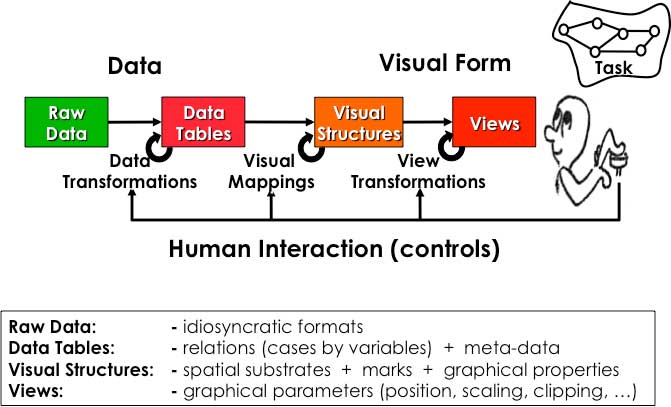
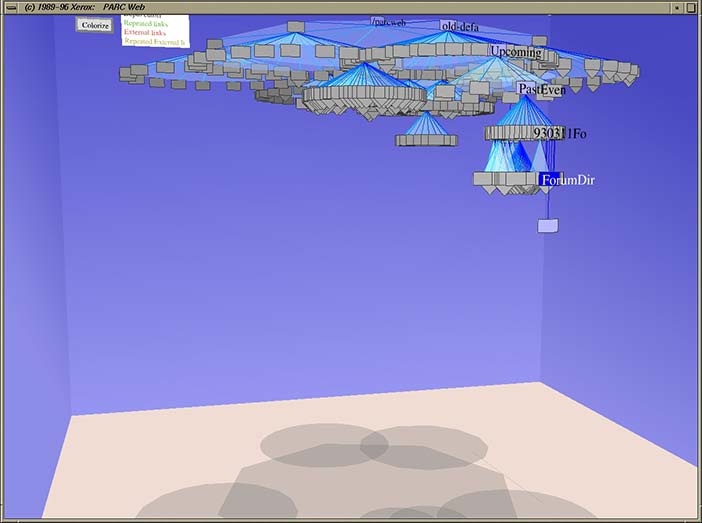
The Bifocal Display is an information presentation technique which allows a large data space to be viewed as a whole, while simultaneously a portion is seen in full detail. The detail is seen in the context of the overview, with continuity across the boundaries, rather than existing in a disjoint window (see Figure 1).
Author/Copyright holder: Robert Spence and Prentice Hall. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in thecopyright terms below.
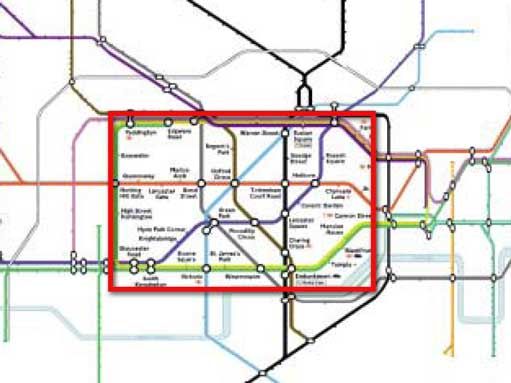
Figure 7.1: A bifocal representation of the London Underground map, showing the central area in full detail, while retaining the context of the entire network. It is important to note the continuity of the lines between the focus and context regions, in spite of the differing magnification factors
William Farrand's (Farrand 1973) observation that "an effective transformation [of data] must somehow maintain global awareness while providing detail" reflected a longstanding concern, both with a user's need to be aware of context and with the "too much data, too small a screen" problem. Although static solutions already existed in the field of geography, an interactively controlled transformation that satisfied Farrand's requirement and, moreover, maintained a continuity of information space, was invented in 1980 by Robert Spence (Imperial College London) and Mark Apperley (University of Waikato, New Zealand), who gave it the name 'Bifocal Display'. Since then it has been implemented, generalized, evaluated and widely applied. Today there are many applications of the Bifocal Display concept in use; for example the very familiar stretchable dock of application icons associated with the Mac OSX (Modine 2008) operating system (Figure 2).

Author/Copyright holder: Apple Computer, Inc. Copyright terms and licence: All Rights Reserved. Used without permission under the Fair Use Doctrine (as permission could not be obtained). See the "Exceptions" section (and subsection "allRightsReserved-UsedWithoutPermission") on the pagecopyright notice.
Figure 7.2: The very familiar example of the bifocal concept; the Macintosh OSX application 'dock', released in 2001
Author/Copyright holder: Courtesy of Rikke Friis Dam and Mads Soegaard. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported).
Introduction to the Bifocal Display
Author/Copyright holder: Courtesy of Rikke Friis Dam and Mads Soegaard. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported).
Main guidelines and future directions
Author/Copyright holder: Courtesy of Rikke Friis Dam and Mads Soegaard. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported).
How the Bifocal Display was invented and launched
Author/Copyright holder: Mark Apperley and Robert Spence. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
The Bifocal Display concept video from 1980
7.1 The Bifocal Display Explained
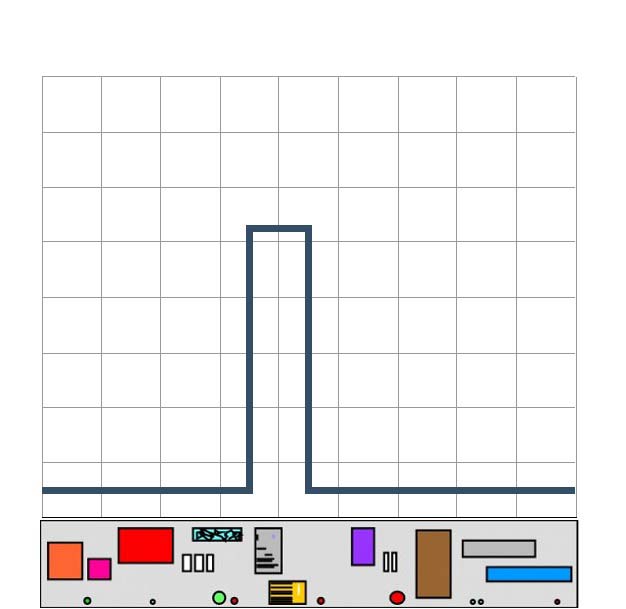
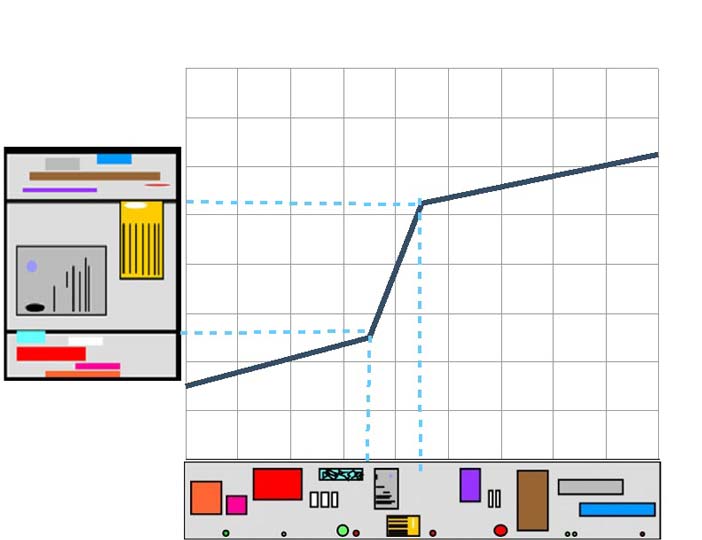
The concept of the Bifocal display can be illustrated by the physical analogy shown in Figures 3, 4, and 5. In Figure 3 we see a sheet representing an information space containing many items: documents, sketches, emails and manuscripts are some examples. As presented in Figure 3 the information space may be too large to be viewed in its entirety through a window, and scrolling would be needed to examine all information items. However, if the sheet representing the information space is wrapped around two uprights, as in Figure 4, and its extremities angled appropriately, a user will see Figure 5 part of the information space in its original detail and, in addition, a 'squashed' view of the remainder of the information space. The squashed view may not allow detail to be discerned but, with appropriate encoding (e.g., colour, vertical position) both the presence and the nature of items outside the focus region can be interpreted. If an item is noticed in the context region and considered to be potentially of interest, the whole information space can be scrolled by hand to bring that item into detail in the focus region.
Figures 3, 4, and 5 emphasises that the 'stretching' or 'distorting' of information space is central to the concept of the Bifocal Display. The continuity of information space between focus and context regions is a vital feature and especially valuable in the context of map representation (see below).

Author/Copyright holder: Courtesy of Mark D. Apperley and Robert Spence. Copyright terms and licence: CC-Att-ND-3 (Creative Commons Attribution-NoDerivs 3.0 Unported).
Figure 7.3: An information space containing documents, email, etc.
Author/Copyright holder: Courtesy of Mark D. Apperley and Robert Spence. Copyright terms and licence: CC-Att-ND-3 (Creative Commons Attribution-NoDerivs 3.0 Unported).
Figure 7.4: The same space wrapped around two uprights

Author/Copyright holder: Courtesy of Mark D. Apperley and Robert Spence. Copyright terms and licence: CC-Att-ND-3 (Creative Commons Attribution-NoDerivs 3.0 Unported).
Figure 7.5: Appearance of the information space when viewed from an appropriate direction
Immediately following its invention in 1980, the Bifocal Display concept was illustrated in a press release based on an (the first!) envisionment video (Apperley and Spence 1980) showing it in use in the scenario of a futuristic office. It was presented to experts in office automation in 1981 (Apperley and Spence 1981a; Apperley and Spence 1981b;) and the technical details (Apperley et al. 1982) of a potential implementation were discussed in 1982, the same year that a formal journal paper (Spence and Apperley 1982) describing the Bifocal display was published.
A number of significant features of the Bifocal display can be identified:
7.1.1 Continuity
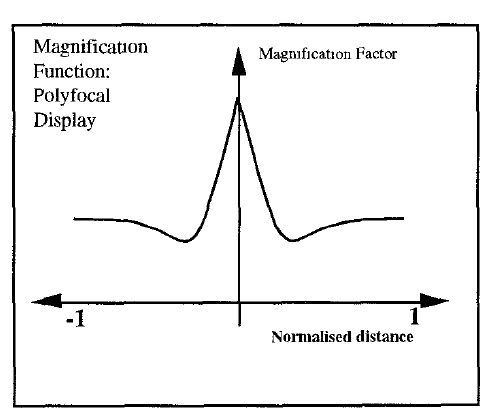
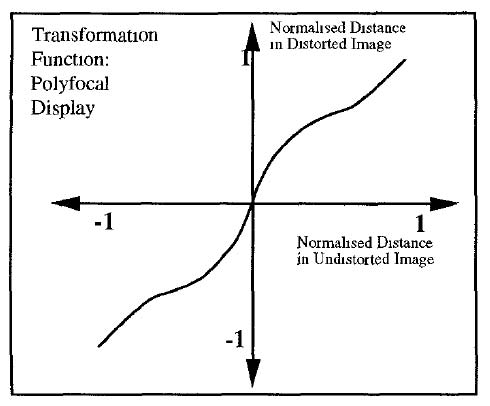
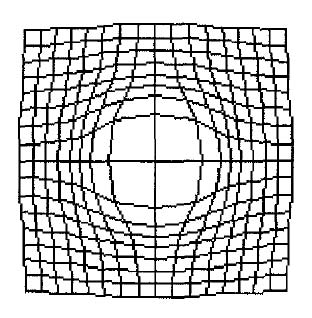
Continuity between the focus and context regions in a bifocal representation is an important and powerful feature, facilitated by the notion of 'stretching' or 'distorting' the information space. Formally, the transformation of the space must be monotonic (effectively, moving in the same direction) in both dimensions for continuity to be visible. In fact, the concept of stretching can be generalised. If the stretching shown in Figures 5, 6, and 7 can be termed X-distortion, then stretching in both directions (XY-distortion) can be advantageous in, for example, the display of calendars (Figure 6) and metro maps (Figure 1): in both these applications the continuity of information space is a distinct advantage. The term 'rubber-sheet stretching' (Tobler 1973; Mackinlay et al. 1991; Sarkar et al. 1993) was seen to neatly explain both the graphical/topological distortion and continuity aspects of focus-plus-context presentations. It is possible that the latter freedom led to use of the term 'fish-eye display' as synonymous with 'bifocal display'. Note that the taxonomy developed by Ying Leung and Apperley (Leung and Apperley 1993a; Leung and Apperley 1993b) discusses the relationships and differences between the bifocal and fish-eye concepts.
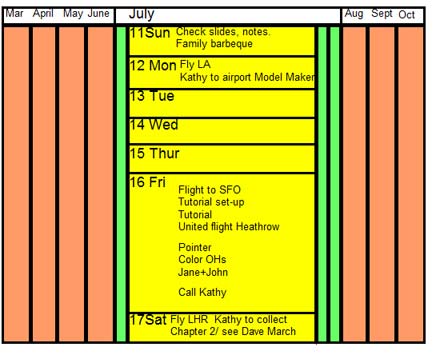
Author/Copyright holder: Courtesy of Bob Spence. Copyright terms and licence: CC-Att-ND-3 (Creative Commons Attribution-NoDerivs 3.0 Unported).
Figure 7.6: Combined X- and Y- distortion provides a convenient calendar interface
7.1.2 Detail Suppression
A second significant feature of the bifocal display is the ability to customise the representation of an item for its appearance in the context region, where fine detail is irrelevant or even inappropriate (see, for example, the London Underground map of Figure 1, where no attempt is made to provide station detail in the context region). The concept of 'degree of interest', later to be formalised by George Furnas (Furnas 1986) might, for example lead to the suppression of text and the possible introduction of alternative visual cues, such as shape and colour, with a view to rendering the item more easily distinguished when in the context region. Whereas the bifocal concept is primarily explained as a presentation technique, it was immediately apparent that the effectiveness of the presentations could be enhanced by corresponding variations in representation, utilising the implicit degree of interest of the focus and context regions.
7.1.3 Interaction: scrolling/panning
Yet a third feature of the bifocal concept concerned manual interaction with the display to achieve scrolling or panning. In the envisionment video (Apperley and Spence 1980) the user is seen scrolling by touch, immediate visual feedback ensuring easy positioning of a desired item in the focus region (see Figure 7). Truly direct manipulation, as in touch, is vital for predictable navigation in a distorted space, and overcomes the issues of scale and speed (Guiard and Beaudouin-Lafon 2004) typically associated with combined panning and zooming operations. The impact and potential of multi-touch interfaces in such interaction is mentioned later.

Author/Copyright holder: Courtesy of Robert Spence, with the assistance of Colin Grimshaw of the Imperial College TV studio. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported)
Figure 7.7: Direct interaction with the Bifocal Display allows a specific item or area to be dragged into the focus region (from Video 5)

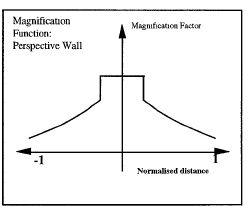
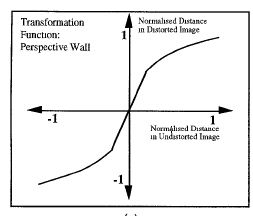
Author/Copyright holder: Courtesy of Inxight Software, Inc (screenshot of Perspective Wall). Copyright terms and licence: Unknown (pending investigation). See section "Exceptions" in the copyright terms below.
Figure 7.8: The Perspective Wall from 1991 has much in common with the bifocal display.
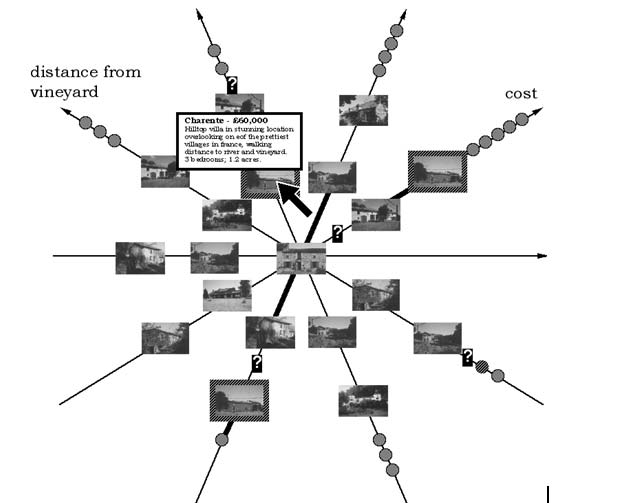
Author/Copyright holder: Courtesy of Mark D. Apperley and Robert Spence. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported).
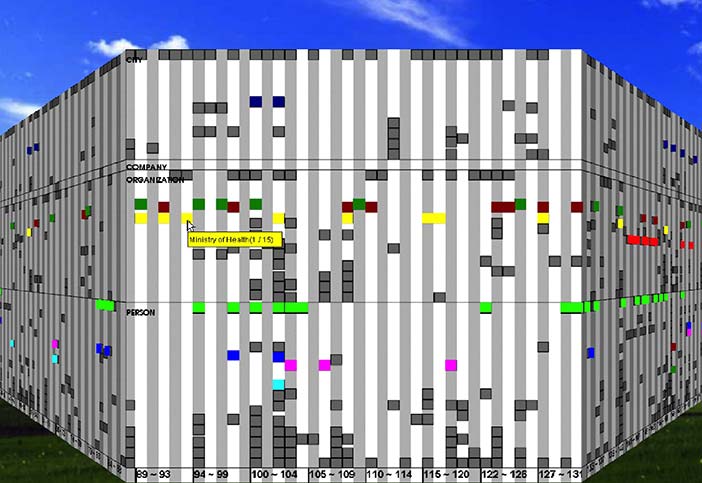
Figure 7.9: The Neighbourhood Explorer (Spence 2001; Apperley et al. 2001). Properties further away from the object of interest on each axis are shown as icons with little detail.
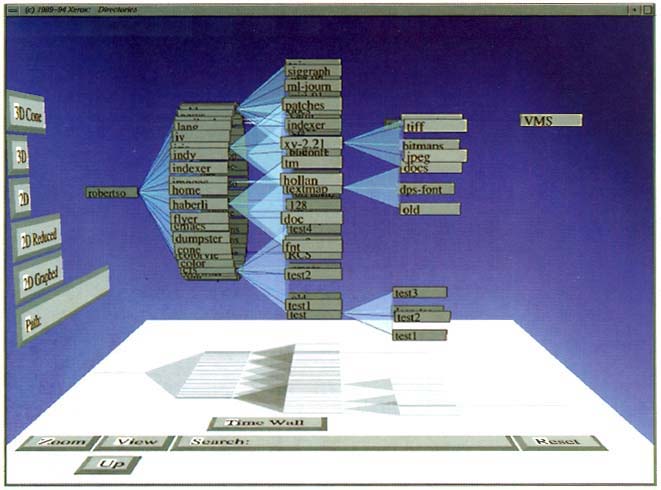
Later work by Apperley and Spence and colleagues described generalizations of the Bifocal Display concept and a useful taxonomy (Leung and Apperley 1993a,b,c,d; Leung et al. 1995). In 1991 a three-dimensional realization of the Bifocal Display, termed the Perspective Wall (Figure 8), was described (Mackinlay et al. 1991). In the Neighbourhood Explorer (Figure 9), Apperley and Spence applied the Bifocal Display concept to the task of home-finding (Spence 2001, page 85; Apperley et al. 2001) in a multi-axis representation. A very effective application of the Bifocal concept to interaction with hierarchically structured data was described by John Lamping and Ramana Rao (Lamping and Rao 1994) who employed a hyperbolic transformation to ensure that, theoretically, an entire tree was mapped to a display (Figure 10). In the same year, Rao and Stuart Card (Rao and Card 1994) described the Table Lens (Figure 12) which, also, employed the concept of stretching.
Author/Copyright holder:Courtesy of Robert Spence. Copyright terms and licence: CC-Att-ND (Creative Commons Attribution-NoDerivs 3.0 Unported).
Figure 7.10: A sketch illustration of the hyperbolic browser representation of a tree. The further away a node is from the root node, the closer it is to its superordinate node, and the area it occupies decreases (Spence 2001)
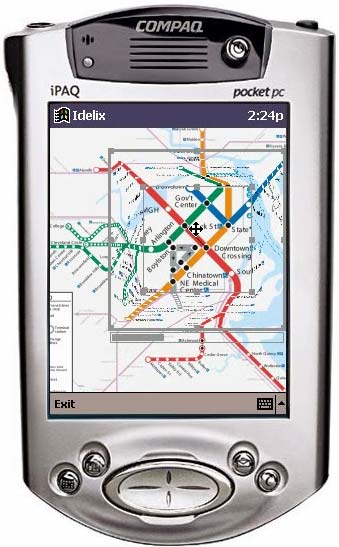
Author/Copyright holder: David Baar, IDELIX Software Inc. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in thecopyright terms below.
Figure 7.11: Distorted map on a PDA, showing the continuity of transportation links
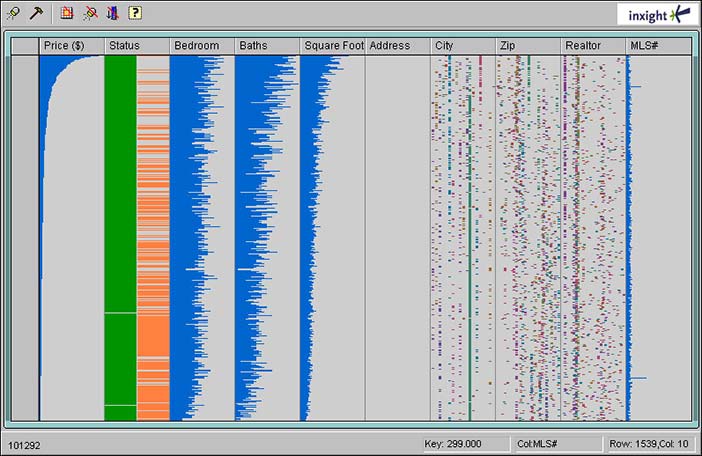
Author/Copyright holder: Courtesy of Inxight Software, Inc (screenshot of Table Lens). Copyright terms and licence: Unknown (pending investigation). See section "Exceptions" in the copyright terms below.
Figure 7.12: Screenshot of the Table Lens. The Table Lens incorporates the concept of stretching in both X and Y dimensions to provide focus plus context (Rao and Card 1994)
The commercial development by IDELIX of software that would implement the concept of the Bifocal Display allowed that company to demonstrate the concept in a number of applications. In one, a transportation map of the Boston area could be examined on the limited display area of a PDA (Figure 11) through the appropriate manual control of panning and variable stretching; automatic degree-of-interest adjustment was employed to make the best use of available display area. By contrast, another application (Figures 13 and 14) employed a table-top display, with four simultaneous users independently controlling the stretching of different areas of the map in order to inspect detail. The value of the Bifocal Display concept to a user's interaction with a calendar was demonstrated by Ben Bederson, Aaron Clamage, Mary Czerwinski and George Robertson (Bederson et al 2004) - see Figure 15.
In a medical application of the bifocal concept a 3D image of a portion of the brain has been distorted to focus on the region around an aneurysm, with the surrounding network of arteries as the context (Cohen et al. 2005) - see Figure 16 and Figure 17.
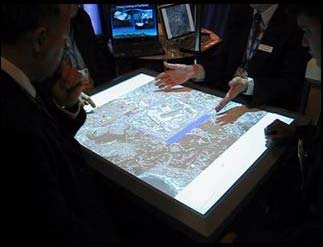
Author/Copyright holder: Unknown (pending investigation). Copyright terms and licence: Unknown (pending investigation). See section "Exceptions" in the copyright terms below.
Figure 7.13: Distorted map on a table (from 2005)

Author/Copyright holder: Clifton Forlines, Chia Shen, and Mitsubishi Electric Research Labs. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Figure 7.14: Distorted map on a table (from 2005)
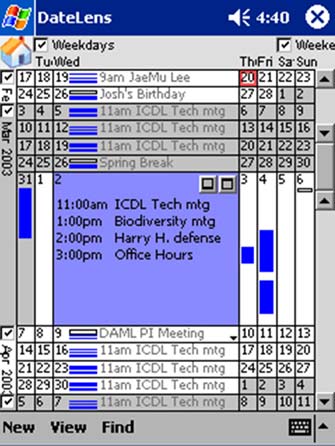
Author/Copyright holder: Bederson et al. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Figure 7.15: Use of the Bifocal Display concept in a PDA-based calendar (Bederson et al. 2004)
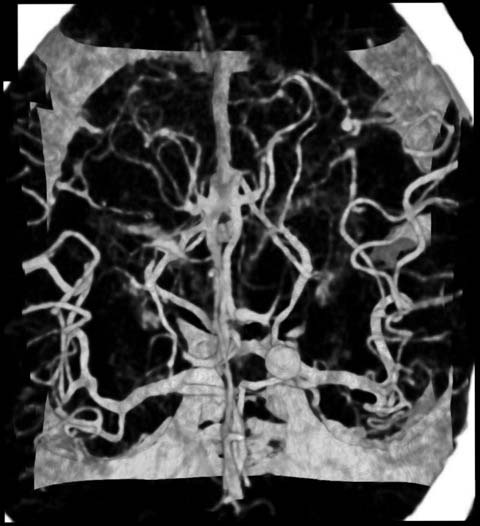
Author/Copyright holder: IEEE, Marcelo Cohen, Ken Brodlie, and Nick Phillips. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Figure 7.16: A 3D medical dataset of a brain aneurysm without bifocal distortion (Cohen et al. 2005)
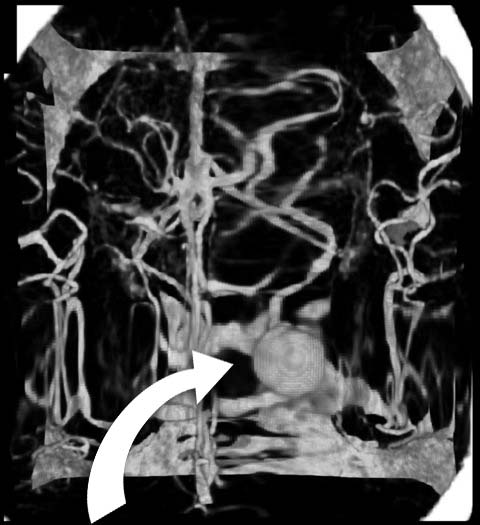
Author/Copyright holder: IEEE, Marcelo Cohen, Ken Brodlie, and Nick Phillips. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Figure 7.17: Bifocal distortion applied to the dataset (Cohen et al. 2005)
7.2 The Future
Research is needed into the fundamental cognitive and perceptual reasons why, and in what circumstances, awareness of context is particularly useful, so that the potential of the bifocal, Degree-of-Interest and other focus+context techniques, alone or in concert, can be assessed for a specific application. The advent of multi-touch screens, and their associated (extreme) direct manipulation, has opened enormous opportunities for improved interaction techniques in navigating large spaces. The single gesture combined pan-zoom operation possible with a multi-touch display offers exciting possibilities for further development and utilisation of the bifocal concept (Forlines and Shen 2005).
7.3 Where to learn more
A chapter of Bill Buxton's book (Buxton 2007) is devoted to the Bifocal Display. The bifocal concept is also treated in many texts associated with Human-computer Interaction, under a variety of index terms: distortion (Ware 2007), bifocal display (Spence 2007; Mazza 2009), and focus+context Tidwell (Tidwell 2005).
7.4 Videos
Appreciation of the Bifocal Display concept can be helped by viewing video presentations. A selection is given below.
Author/Copyright holder: Unknown (pending investigation). Copyright terms and licence: Unknown (pending investigation). See section "Exceptions" in the copyright terms below.
The Bifocal Display
Author/Copyright holder: Robert Spence. Copyright terms and licence: ll Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
The Bifocal Display
Author/Copyright holder: IDELIX Software. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Distorted map on a PDA (52 seconds, silent)
Author/Copyright holder: Clifton Forlines, Chia Shen and Mitsubishi Electric Research Labs. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Pliable display Technology on a table (3 minutes)
Author/Copyright holder: IDELIX Software. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
Rubber sheet map distortion (33 seconds, silent)
Author/Copyright holder: Jock D. Mackinlay, George D. Robertson and Stuart K. Card. Copyright terms and licence: All Rights Reserved. Reproduced with permission. See section "Exceptions" in the copyright terms below.
The Perspective Wall (54 seconds)
7.5 References
Apperley, Mark and Leung, Y. K. (1993b): A taxonomy of distortion-oriented techniques for data presentation. In:Salvendy, Gavriel and Smith, M. J. (eds.). "Advances in Human Factors/Ergonomics Vol 19B, Human-Computer Interaction: Software and Hardware Interfaces". Amsterdam, Holland: Elsevier Science Publisherspp. 105-109
Apperley, Mark and Leung, Y. K. (1993a). A Unified Theory of Distortion-Oriented Presentation Techniques. Massey University
Apperley, Mark and Spence, Robert (1980). Video: bifocal display concept video. Retrieved 4 November 2013 from https://www.interaction-design.org/tv/bifocal_displ...
Apperley, Mark and Spence, Robert (1981): A Professional's Interface Using the Bifocal Display. In: Proceedings of the 1981 Office Automation Conference 1981. pp. 313-315
Apperley, Mark, Spence, Robert and Wittenburg, Kent (2001): Selecting One from Many: The Development of a Scalable Visualization Tool. In: HCC 2001 - IEEE CS International Symposium on Human-Centric Computing Languages and Environments September 5-7, 2001, Stresa, Italy. pp. 366-372
Apperley, Mark, Tzavaras, I. and Spence, Robert (1982): A Bifocal Display Technique for Data Presentation. In:Eurographics 82 Proceedings 1982, Amsterdam. pp. 27-43
Bederson, Benjamin B., Clamage, Aaron, Czerwinski, Mary and Robertson, George G. (2004): DateLens: A fisheye calendar interface for PDAs. In ACM Transactions on Computer-Human Interaction, 11 (1) pp. 90-119
Buxton, Bill (2007): Sketching User Experiences: Getting the Design Right and the Right Design. Morgan Kaufmann
Cohen, Marcelo, Brodlie, Ken and Phillips, Nick (): Hardware-accelerated distortion for volume visualisation in medicine. In: Proceedings of the 4th IEEE EMBSS UKRI PG Conference on Biomedical Engineering and Medical Physics 2005 . pp. 29-30
Farrand, William A. (1973). Information display in interactive design, Doctoral Thesis. University of California at Los Angeles
Forlines, Clifton and Shen, Chia (2005): DTLens: multi-user tabletop spatial data exploration. In: Proceedings of the 2005 ACM Symposium on User Interface Software and Technology 2005. pp. 119-122
Furnas, George W. (1986): Generalized Fisheye Views. In: Mantei, Marilyn and Orbeton, Peter (eds.) Proceedings of the ACM CHI 86 Human Factors in Computing Systems Conference April 13-17, 1986, Boston, Massachusetts. pp. 16-23
Guiard, Yves and Beaudouin-Lafon, Michel (2004): Target acquisition in multiscale electronic worlds. InInternational Journal of Human-Computer Studies, 61 (6) pp. 875-905
Lamping, John and Rao, Ramana (1994): Laying Out and Visualizing Large Trees Using a Hyperbolic Space. In:Szekely, Pedro (ed.) Proceedings of the 7th annual ACM symposium on User interface software and technologyNovember 02 - 04, 1994, Marina del Rey, California, United States. pp. 13-14
Leung, Ying K. and Apperley, Mark (1993): E{cubed}: Towards the Metrication of Graphical Presentation Techniques for Large Data Sets. In: East-West International Conference on Human-Computer Interaction: Proceedings of the EWHCI93 1993. pp. 9-26
Leung, Ying K. and Apperley, Mark (1993): Extending the Perspective Wall. In: Proceedings of OZCHI93, the CHISIG Annual Conference on Human-Computer Interaction 1993. pp. 110-120
Leung, Y. W. and Apperley, Mark (1994): A Review and Taxonomy of Distortion-Oriented Presentation Techniques. In ACM Transactions on Computer-Human Interaction, 1 (2) pp. 126-160
Leung, Ying K., Spence, Robert and Apperley, Mark (1995): Applying Bifocal Displays to Topological Maps. InInternational Journal of Human-Computer Interaction, 7 (1) pp. 79-98
Mackinlay, Jock D., Robertson, George G. and Card, Stuart K. (1991): The Perspective Wall: Detail and Context Smoothly Integrated. In: Robertson, Scott P., Olson, Gary M. and Olson, Judith S. (eds.) Proceedings of the ACM CHI 91 Human Factors in Computing Systems Conference April 28 - June 5, 1991, New Orleans, Louisiana. pp. 173-179
Mazza, Riccardo (2009): Introduction to Information Visualization. Springer
Modine, Austin (2008). Apple patents OS X Dock. Retrieved 9 November 2010 from The Register: http://www.theregister.co.uk/2008/10/08/apple_pate...
Rao, Ramana and Card, Stuart K. (1994): The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+Context Visualization for Tabular Information. In: Adelson, Beth, Dumais, Susan and Olson, Judith S. (eds.) Proceedings of the ACM CHI 94 Human Factors in Computing Systems Conference April 24-28, 1994, Boston, Massachusetts. pp. 318-322
Sarkar, Manojit, Snibbe, Scott S., Tversky, Oren J. and Reiss, Steven P. (1993): Stretching the Rubber Sheet: A Metophor for Visualizing Large Layouts on Small Screens. In: Hudson, Scott E., Pausch, Randy, Zanden, Brad Vander and Foley, James D. (eds.) Proceedings of the 6th annual ACM symposium on User interface software and technology 1993, Atlanta, Georgia, United States. pp. 81-91
Spence, Robert (2007): Information Visualization: Design for Interaction (2nd Edition). Prentice Hall
Spence, Robert (2001): Information Visualization. Addison Wesley
Spence, Robert and Apperley, Mark (1982): Data Base Navigation: An Office Environment for the Professional. InBehaviour and Information Technology, 1 (1) pp. 43-54
Tidwell, Jenifer (2005): Designing Interfaces: Patterns for Effective Interaction Design. O'Reilly and Associates
Tobler, W. R. (1973): A continuous transformation useful for districting. In Annals of the New York Academy of Sciences, 219 p. 215–220
Ware, Colin (2004): Information Visualization: Perception for Design, 2nd Ed. San Francisco, Morgan Kaufman