If we were to give you $1,000 today or a promise to pay you $1,000 in one year’s time which would you choose? Well, assuming that you aren’t aware of a specific requirement to pay someone $1,000 in a year’s time and that you don’t think you can meet that obligation – you’re going to choose $1,000 today. That’s because $1,000 today is worth more than $1,000 in a year’s time.
Why is $1,000 today worth more than $1,000 in a year’s time? Well, firstly there’s the fact that you could invest that $1,000 today and in a year it will be worth more than $1,000, assuming you invest wisely. Secondly, there is the effect of inflation. Inflation is a measure of the rise in cost of goods and services and in most instances – inflation will be positive over the course of a year. That means once a year has passed you can buy less goods and services for $1,000 than you could for $1,000 today.
So it’s pretty easy to make the decision to take the $1,000 today. You know it will be worth more than $1,000 in a year’s time.
However, now imagine that we are offering you $1,000 today or $1,100 in a year’s time. We know that $1,000 will be worth less than it is today in 1 years’ time but would an extra $100 in a year’s time make up for that? Is it possible that $1,100 in a year’s time is worth more than $1,000 today and if so, how much more?
What about if we offered you $1,000 today or $2,000 in 3 years’ time? It’s not so easy to work out which is the best option is it? So how do we tackle the question of value over time?
Future Value
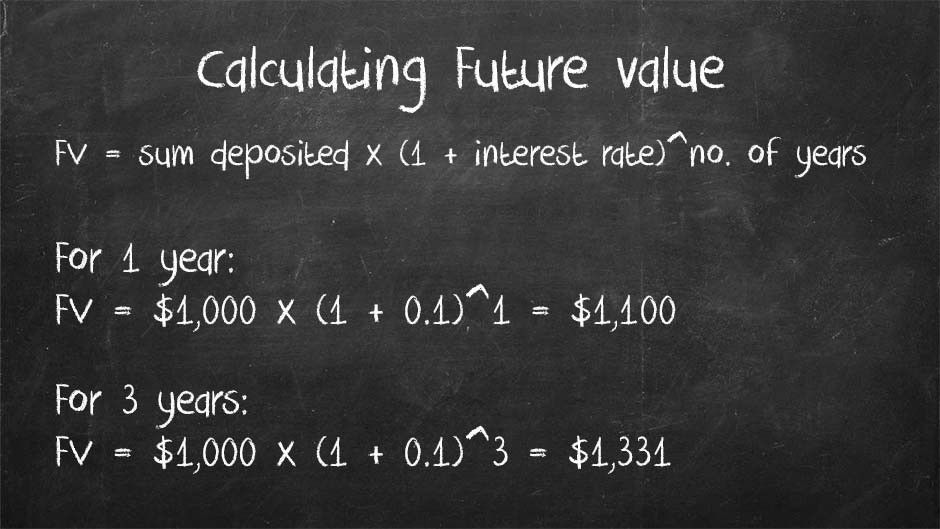
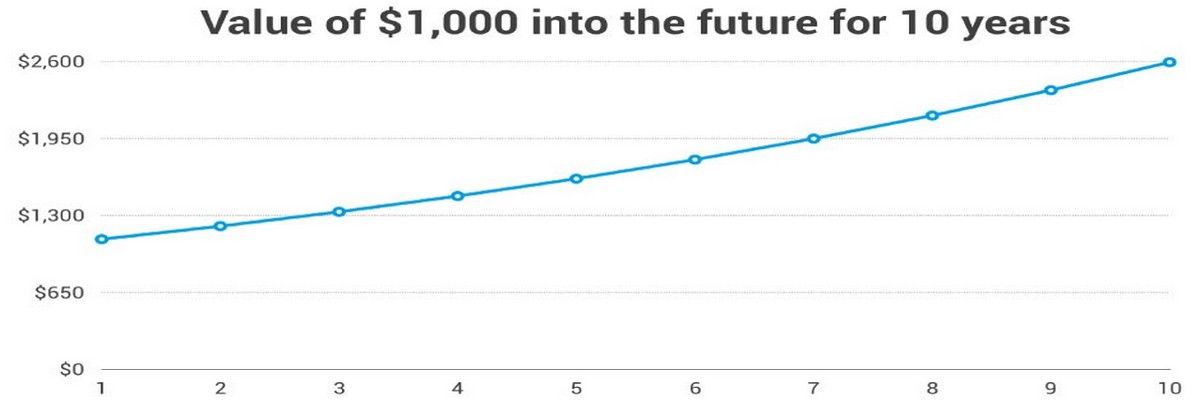
Let’s take our $1,000 today and see what that might be worth in a year’s time or indeed, in 3 years’ time.
We go and talk to our bank manager and they say that they can provide a simple savings account. It pays interest of 10% p.a. and that interest is compounded each year after the first. (Compound interest is when the bank pays interest on the interest that it has paid you already. Simple interest, on the other hand, is only paid against the original sum deposited and any interest earned is ignored in future years).
We need to calculate the future value of our $1,000 in 1 years’ time and in 3 years’ time. How do we do this?
Future Value (FV) can be calculated in two ways:
For an asset with simple annual interest: FV = Sum Deposited x ((1 + (interest rate * number of years))
For an asset with compound annual interest: FV = Sum Deposited x ((1 + interest rate)^number of years))
That ^ symbol means “to the power of”.
We are going to invest our $1,000 for 1 year in our first example.
That means our sum deposited = $1,000 and the interest rate is 0.1 and number of years is 1
FV = $1000 x (1 + 0.1)^1 = $1,100
That means in 1 years’ time $1,000 will have a future value (FV) of $1,100. So if we have offered you $1,000 now or $1,100 in 1 years’ time and you can get 10% interest on your savings – we’ve offered you exactly the same future value as the money we’ve offered today. You are no better off and no worse off for accepting our offer of being paid $1,100 in a year’s time rather than taking $1,000 now.
In our second example we’re going to invest $1,000 for 3 years. Let’s take a look at that now:
That means our sum deposited = $1,000 and the interest rate is 0.1 and number of years is 3
FV = $1,000 x (1 + 0.1)^3 = $1,331
That means in 3 years’ time our $1,000 will have a future value of $1,331. So if we offered you $2,000 in 3 years’ time and the best interest rate you can get is 10% on your savings; you’d be better off waiting for us to pay you $2,000 than taking $1,000 today.
Present Value

Present value lets us take a future value and put it in today’s terms. This can be very important in business and in life. Let’s say that you have a life insurance policy which is due to pay out $500,000 in 5 years’ time. Unfortunately, you need money today. Luckily, you have a wealthy friend who has agreed to buy out your life insurance policy for what it’s worth today – they don’t expect to make a profit but they don’t want to lose money on the deal. How much do you sell them your life insurance policy for?
We need to calculate that present value to ensure that we neither cheat our friend nor ourselves. So how do we do that?
Well, there are many models for present value but the most common is one based on compound interest. Let’s assume our friend can put his money in a savings account which pays out 10% compound interest annually.
Present Value (PV) = C/(1+i)^n
Where C is the future sum of money, the i is the interest rate and n is the number of years.
So for our $500,000, the interest rate is 0.1 and the number of years is 5.
PV = $500,000/(1+0.1)^5 = $500,000/1.61 = $310, 559
That means if your friend put $310,599 in the bank at an interest of 10% compound annually and waited 5 years he would receive $500,000. It also means that your life insurance policy is only worth $310,599 in today’s terms to your friend.
Of course if you were selling a life insurance policy with a fixed payout – it’s unlikely that you would have such a kind friend standing by to pay for your policy. Most people who buy policies with maturity dates in the future – expect to make a profit. Normally, you would find that you would have to sell your policy for quite a bit less than $310,599 to make it attractive to someone else.
This is important because if you know the present value of your life insurance policy; you can negotiate the best deal for yourself. No-one is going to pay more than that $310,599 because then they would lose money but you can try and keep them as close to that figure as possible.
The Take Away

The concepts of present and future value enable us to compare the value of two sums of money in two different periods of time. In a rational world; these calculations would be what drove our choices with respect to value. When offered $1,000 today or $2,000 in 3 years’ time – we’d take the $2,000 in 3 years’ time because we know that $1,000 today (assuming 10% compound interest is available to us) is only worth $1,331 in 3 years’ time.
Why does this matter to designers? Firstly, it matters in everyday life because it allows you to make rational decisions about value over time. Secondly, it matters in your designs because if your design provides value in the future (rather than immediately) you will need to provide much more value in the future than a design which provides value immediately. This is because, generally, value decreases over time.
It’s worth noting that the concept of present value also moves beyond design as J R Rim the investor says; “Investing is a simple process of taking into account the present value and future value.” So maybe you can put it into practice elsewhere too.
References
You can learn more about present value and other ways of handling these calculations here.
You can learn more about future value and other ways of handling these calculations here.