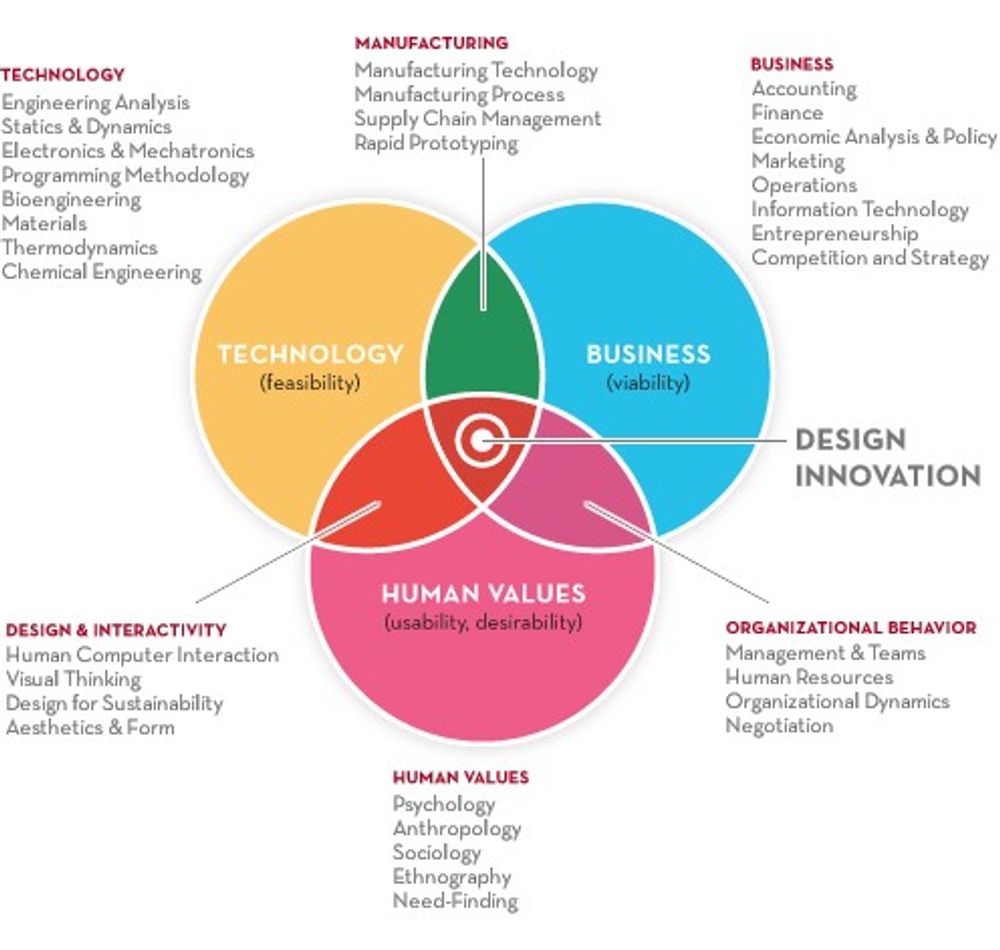
"Formal methods" sounds kind of scary but it in reality it’s a way of saying; “the system with which we record ideas/information/etc.” and that’s rather less scary. In Human Computer Interaction (HCI) there are a multitude of formal methods, in use, to record ideas and other types of information. Today, we’ll take a look at the three main types of formal method and then we may look at the methods themselves in more detail in another article at a later date.
The Three Types of Formal Methods for HCI
Users
It perhaps comes as no surprise that there are formal methods dedicated to capturing what goes on at the user-level. This is of course, the reason that we all do what we do. Without users any HCI (or indeed User Interface/UI) work is wasted. If no-one uses the product; who cares what it does? There’s a time and a place for theory but once we’re doing design work – it’s not about theory it’s about practice.
![]()
What may come as a bit of a surprise is there are no commonly used formal methods for dealing with groups of users at higher levels. Use there are task-modelling systems, for example, which deal with more than one user but there are no in depth formal methods for social-level modelling or demographic-level modelling.
Systems
If you have a formal method for documenting the user’s approach to a product; you also need a method for documenting the system level too. That is not just the user's interaction with that system but what happens during that interaction "out of sight" of the user. Choosing to represent the system rather than the user does not mean that we have not taken the user into account; it’s rather that we sometimes need to document what is happening and why in different ways. This also gives us the opportunity to examine the back-end of the model as well as the front-end.
World
This might be better described as contextual or environmental; it’s often important to examine the physical context of a user’s interaction with a product. It’s all well and good designing a system to make it easier for someone in a wheelchair to use a computer but if in the real work environment; that computer is not positioned in a wheelchair accessible zone – it’s not going to deliver the benefits that we hope for. It's important to understand where and how our systems are used not just the people who use them.
![]()
We may also want to model user flow for systems which will have large volumes of users; how will they get to the product? How will they leave? What incentives do they need to do this efficiently? And so on…
In Combination
Of course all of these formal methods can be used in combination but in general they will be used in different ways and at different levels in your system's documentation. If you want to learn more about Formal Methods and their use; you can find Alan J Dix’s book here. Alan’s a Computing Professor at Lancaster University in the UK.
References & Where to Learn More:
Header Image: Author/Copyright holder: aknottedcord.Copyright terms and licence: All rights reserved. Img
Course: “Human-Computer Interaction - The Foundations of UX Design”
Images: Header, HCI, Users, World